847. Shortest Path Visiting All Nodes
1. Question
You have an undirected, connected graph of n nodes labeled from 0ton - 1. You are given an array graph where graph[i] is a list of all the nodes connected with node i by an edge.
Return the length of the shortest path that visits every node. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.
2. Examples
Example 1:
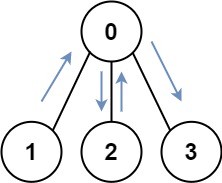
Input: graph = [[1,2,3],[0],[0],[0]]
Output: 4
Explanation: One possible path is [1,0,2,0,3]
Example 2:
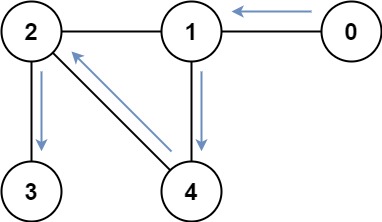
Input: graph = [[1],[0,2,4],[1,3,4],[2],[1,2]]
Output: 4
Explanation: One possible path is [0,1,4,2,3]
3. Constraints
n == graph.length1 <= n <= 120 <= graph[i].length < ngraph[i]does not containi.- If
graph[a]containsb, thengraph[b]containsa. - The input graph is always connected.
4. References
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/shortest-path-visiting-all-nodes 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
5. Solutions
参考。
class Solution {
public int shortestPathLength(int[][] graph) {
/**
* 思路:
* 利用广度优先从每个节点出发进行搜索。搜索到任意节点时,保存已经经历过的节点。
* 已经经历过的节点不需要保存顺序,因为采用的是广度优选搜索,所以第一次搜索到此状态的路径一定是最短的。
* 所有节点都搜完时,结束搜索
*/
int len = graph.length;
// 记录访问某个节点时,已经访问过的节点集合(状态),每个bit表示一个节点
// 由于采用的是广度优选搜索,所以走过已经访问过的节点的路径一定是最短的
boolean[][] visited = new boolean[len][1 << len];
// 记录正在搜索的中间状态
// queue中的元素为有两个元素的数组:节点,访问此节点对应的状态
Queue<int[]> queue = new LinkedList<>();
for (int i = 0; i < len; i++) {// 从每个节点出发搜索结果
queue.add(new int[]{i, 1 << i});
}
int step = 0;
int endState = (1 << len) - 1; //当所有节点都走到过之后便可以结束搜索
while (!queue.isEmpty()) {
for (int i = queue.size(); i > 0; i--) {
int[] entry = queue.poll();
int point = entry[0];
int state = entry[1];
for (int next : graph[point]) {
int nextState = state | (1 << next);
if (nextState == endState) {
return step + 1;
}
if (visited[next][nextState]) {
continue;
}
visited[next][nextState] = true;
queue.add(new int[]{next, nextState});
}
}
step++;
}
return 0;//graph为空
}
}