797. All Paths From Source to Target
1. Question
Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n - 1, find all possible paths from node 0 to node n - 1 and return them in any order.
The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).
2. Examples
Example 1:
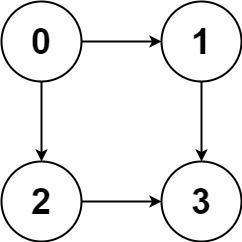
Input: graph = [[1,2],[3],[3],[]]
Output: [[0,1,3],[0,2,3]]
Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.
Example 2:
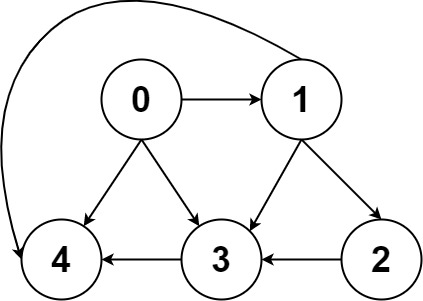
Input: graph = [[4,3,1],[3,2,4],[3],[4],[]]
Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
Example 3:
Input: graph = [[1],[]]
Output: [[0,1]]
Example 4:
Input: graph = [[1,2,3],[2],[3],[]]
Output: [[0,1,2,3],[0,2,3],[0,3]]
Example 5:
Input: graph = [[1,3],[2],[3],[]]
Output: [[0,1,2,3],[0,3]]
3. Constraints
n == graph.length2 <= n <= 150 <= graph[i][j] < ngraph[i][j] != i(i.e., there will be no self-loops).- All the elements of
graph[i]are unique. - The input graph is guaranteed to be a DAG.
4. References
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/all-paths-from-source-to-target 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
5. Solutions
dfs
class Solution {
List<List<Integer>> lists = new ArrayList<>();
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
dfs(graph, 0, new ArrayList<>());
return lists;
}
public void dfs(int[][] graph, int index, List<Integer> list) {
list.add(index);
if (index == graph.length - 1) {
lists.add(new ArrayList<>(list));
return ;
}
for (int i : graph[index]) {
dfs(graph, i, list);
list.remove(list.size() - 1); // 不符合条件的要删掉
}
}
}