787. Cheapest Flights Within K Stops

1. Question

There are n cities connected by some number of flights. You are given an array flights where flights[i] = [from_i, to_i, price_i] indicates that there is a flight from city from_i to city to_i with cost price_i.

You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.

2. Examples

Example 1:

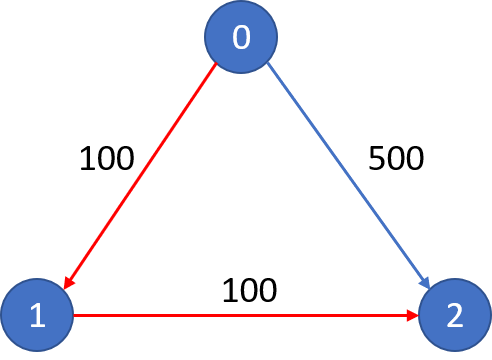
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1
Output: 200
Explanation: The graph is shown.
The cheapest price from city 0 to city 2 with at most 1 stop costs 200, as marked red in the picture.

Example 2:

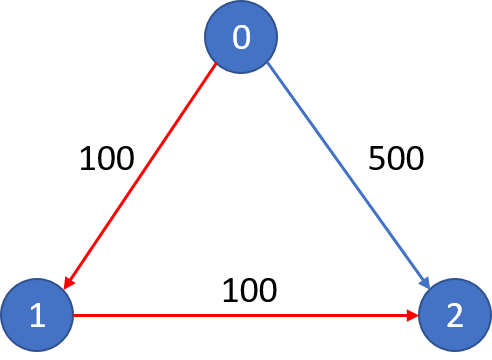
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0
Output: 500
Explanation: The graph is shown.
The cheapest price from city 0 to city 2 with at most 0 stop costs 500, as marked blue in the picture.

3. Constraints:

• 1 <= n <= 100
• 0 <= flights.length <= (n * (n - 1) / 2)
• flights[i].length == 3
• 0 <= from_i, to_i < n
• from_i != to_i
• 1 <= price_i <= 10⁴
• There will not be any multiple flights between two cities.
• 0 <= src, dst, k < n
• src != dst

4. References

来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/cheapest-flights-within-k-stops 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

5. Solutions

dp

class Solution {
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        final int INF = 100_001;
        int[][] f = new int[k + 2][n];
        for (int i = 0; i < f.length; i++) {
            Arrays.fill(f[i], INF);
        }
        f[0][src] = 0;
        for (int times = 1; times < f.length; times++) {
            for (int[] flight : flights) {
                int s = flight[0];
                int d = flight[1];
                int cost = flight[2];
                f[times][d] = Math.min(f[times][d], f[times - 1][s] + cost);
            }
        }
        int res = INF;
        for (int times = 1; times < f.length; times++) {
            res = Math.min(res, f[times][dst]);
        }
        return res == INF ? -1 : res;
    }
}