1. 391. Perfect Rectangle
2. Question
Given an array rectangles where rectangles[i] = [xi, yi, ai, bi] represents an axis-aligned rectangle. The bottom-left point of the rectangle is (xi, yi) and the top-right point of it is (ai, bi).
Return true if all the rectangles together form an exact cover of a rectangular region.
3. Examples
Example 1:
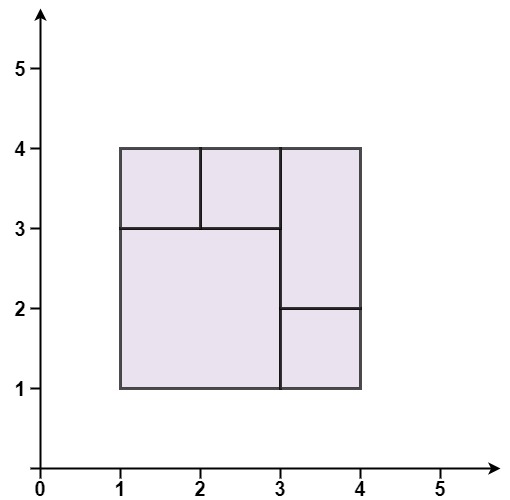
Input: rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
Output: true
Explanation: All 5 rectangles together form an exact cover of a rectangular region.
Example 2:
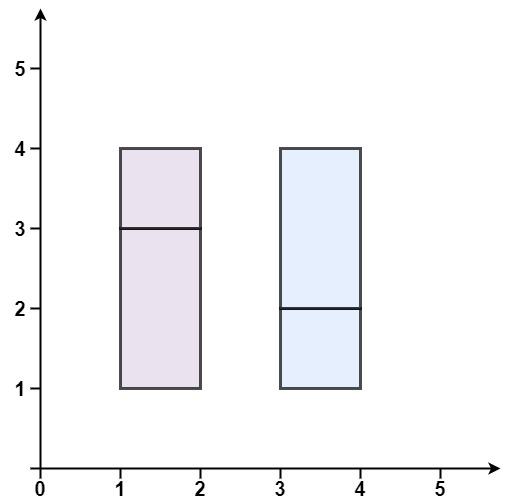
Input: rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
Output: false
Explanation: Because there is a gap between the two rectangular regions.
Example 3:
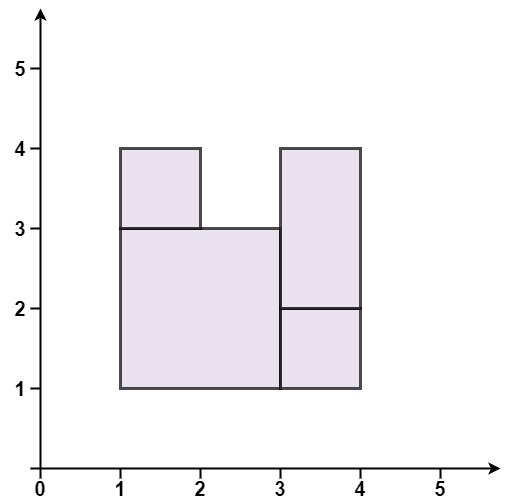
Input: rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[3,2,4,4]]
Output: false
Explanation: Because there is a gap in the top center.
Example 4:
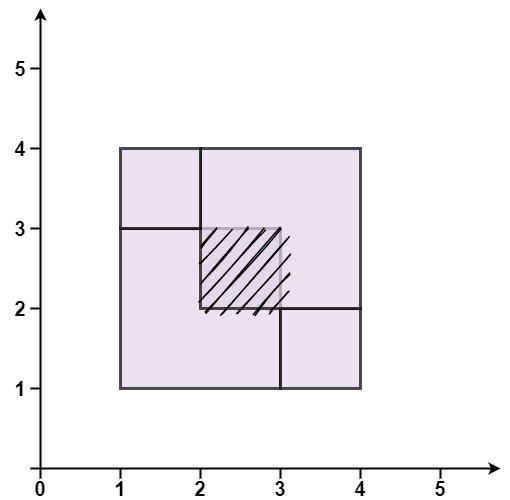
Input: rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]
Output: false
Explanation: Because two of the rectangles overlap with each other.
4. Constraints
- 1 <= rectangles.length <= 2 * 104
rectangles[i].length == 4- -105 <= xi, yi, ai, bi <= 105
5. References
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/perfect-rectangle 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
6. Solutions
class Solution {
public boolean isRectangleCover(int[][] rectangles) {
// 通过面积判断,此处需要设定四个预设值
int left = Integer.MAX_VALUE;
int bottom = Integer.MAX_VALUE;
int right = Integer.MIN_VALUE;
int top = Integer.MIN_VALUE;
// 用于记录最终剩下的顶点
HashSet<String> set = new HashSet<>();
// 用于累加小矩形的坐标
int sum = 0;
for (int i = 0; i < rectangles.length; i++) {
// 获取第i个小矩形的数据
int[] t = rectangles[i];
// 此处计算所有小矩形最终拼接出来的矩形的最大范围
left = Math.min(left, t[0]);
bottom = Math.min(bottom, t[1]);
right = Math.max(right, t[2]);
top = Math.max(top, t[3]);
// 计算面积
sum += getArea(t[0], t[1], t[2], t[3]);
// 记录小矩形的四个顶点的坐标
String[] strings = new String[4];
strings[0] = merge(t[0], t[1]);
strings[1] = merge(t[0], t[3]);
strings[2] = merge(t[2], t[1]);
strings[3] = merge(t[2], t[3]);
// 如果该顶点在所有记录中出现过,则进行删除,如果没有出现过,则插入
// 偶数次抵消(不成角), 奇数次保留(必留有角)
for (int j = 0; j < 4; j++) {
if (set.contains(strings[j])) {
set.remove(strings[j]);
} else {
set.add(strings[j]);
}
}
}
// 最后只留下四个顶点且和最大的矩形的四个顶点对应,则比较面积,均相等则true
if (set.size() == 4 && set.contains(merge(left, top)) && set.contains(merge(left, bottom))
&& set.contains(merge(right, top)) && set.contains(merge(right, bottom))) {
return sum == getArea(left, bottom, right, top);
}
return false;
}
private int getArea(int left, int bottom, int right, int top) {
return (right - left) * (top - bottom);
}
private String merge(int a, int b) {
return a + " " + b;
}
}